728x90
반응형
최대 공약수
최대 공약수는 두 개 이상의 정수의 공통되는 약수중에서 가장 큰 수이다. 예를 들어, 24와 18의 최대 공약수는 6이다. 최대 공약수는 유클리드 호제법을 사용하면 쉽게 구할 수 있다.
유클리드 호제법
유클리드 호제법(- 互除法, Euclidean Algorithm)은 2개의 자연수 또는 정식(整式)의 최대공약수(Greatest Common Divisor)를 구하는 알고리즘의 하나이다. 호제법이란 말은 두 수가 서로(互) 상대방 수를 나누어(除)서 결국 원하는 수를 얻는 알고리즘을 나타낸다.
- 위키백과, 우리 모두의 백과사전.
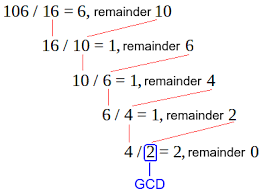
- 두 수 중 큰 수를 작은 수로 나누어 나머지를 구한다. (106 % 16 = 10)
- 작은 수를 방금 구한 나머지로 나눈다. (16 % 10 = 6)
- 나머지가 0이 될때까지 반복한다.
- 나머지가 0이 될 때 나눴던 수가 최대 공약수이다.
유클리드 호제법을 코드로 나타내면 다음과 같다.
private int gcd(int max, int min) {
while (max % min != 0) {
int temp = max;
max = min;
min = temp % min;
}
return min;
}다음과 같이 재귀 함수로도 간단하게 나타낼 수 있다.
public int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
세 개 이상의 수들에 대한 최대 공약수를 구하려면 먼저 두 수의 최대 공약수를 구하고, 최대 공약수와 나머지 수에 대해 다시 최대 공약수를 구하면 된다.
public int multiGcd(int a, int b, int c) {
int gcdAB = gcd(a, b);
return gcd(Math.max(c, gcdAB), Math.min(c, gcdAB));
}
public int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
최소 공배수
최소 공배수는 투 포인터로 값을 늘려가며 찾을 수도 있지만 앞서 살펴본 유클리드 호제법을 이용하여 A * B / 최대 공약수로 쉽게 구할 수 있다.
public int lcm(int a, int b) {
// 최소 공배수 = a * b / 최대 공약수
return a * b / gcd(a, b);
}
public int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
728x90
반응형
728x90
반응형
최대 공약수
최대 공약수는 두 개 이상의 정수의 공통되는 약수중에서 가장 큰 수이다. 예를 들어, 24와 18의 최대 공약수는 6이다. 최대 공약수는 유클리드 호제법을 사용하면 쉽게 구할 수 있다.
유클리드 호제법
유클리드 호제법(- 互除法, Euclidean Algorithm)은 2개의 자연수 또는 정식(整式)의 최대공약수(Greatest Common Divisor)를 구하는 알고리즘의 하나이다. 호제법이란 말은 두 수가 서로(互) 상대방 수를 나누어(除)서 결국 원하는 수를 얻는 알고리즘을 나타낸다.
- 위키백과, 우리 모두의 백과사전.
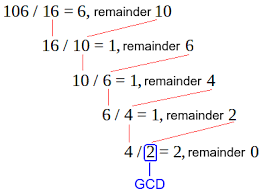
- 두 수 중 큰 수를 작은 수로 나누어 나머지를 구한다. (106 % 16 = 10)
- 작은 수를 방금 구한 나머지로 나눈다. (16 % 10 = 6)
- 나머지가 0이 될때까지 반복한다.
- 나머지가 0이 될 때 나눴던 수가 최대 공약수이다.
유클리드 호제법을 코드로 나타내면 다음과 같다.
private int gcd(int max, int min) {
while (max % min != 0) {
int temp = max;
max = min;
min = temp % min;
}
return min;
}다음과 같이 재귀 함수로도 간단하게 나타낼 수 있다.
public int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
세 개 이상의 수들에 대한 최대 공약수를 구하려면 먼저 두 수의 최대 공약수를 구하고, 최대 공약수와 나머지 수에 대해 다시 최대 공약수를 구하면 된다.
public int multiGcd(int a, int b, int c) {
int gcdAB = gcd(a, b);
return gcd(Math.max(c, gcdAB), Math.min(c, gcdAB));
}
public int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
최소 공배수
최소 공배수는 투 포인터로 값을 늘려가며 찾을 수도 있지만 앞서 살펴본 유클리드 호제법을 이용하여 A * B / 최대 공약수로 쉽게 구할 수 있다.
public int lcm(int a, int b) {
// 최소 공배수 = a * b / 최대 공약수
return a * b / gcd(a, b);
}
public int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
728x90
반응형
