고대 그리스 수학자 에라토스테네스가 발견한 '에라토스테네스의 체'는 2부터 N까지의 범위에서 소수를 구하는 알고리즘이다.
소수를 판별하는 문제에서 매우 유용하게 사용할 수 있다.
1부터 120까지의 숫자중에서 소수인 숫자를 구하려면 어떻게 해야할까?
1부터 120까지 1씩 숫자를 늘려가며 소수인지 판별할 수도 있겠지만 '에라토스테네스의 체' 알고리즘을 사용하면 보다 빠르게 답을 구할 수 있다. 참고로 '에라토스테네스의 체'의 시간 복잡도는 O(n log(logn)) 이다.
'에라토스테네스의 체'의 핵심은 배열에서 소수의 배수를 모두 제거하고 남은 숫자는 모두 소수라는 성질을 이용한 것이다. 아래의 gif를 보자.
- 우선 2부터 N까지의 숫자를 저장하는 배열을 선언한다. 2부터 시작하는 이유는 1은 소수가 아니기 때문이다.
- 소수 : 1과 자신을 제외한 어떠한 자연수로도 나누어 떨어질 수 없는 수.
- 배열 범위 내에 있는 2의 배수를 모두 지운다. 자기 자신은 지우지 않는다. (2는 남김)
- 2 다음에 지워지지 않은 숫자의 배수를 모두 지운다. 마찬가지로 자기 자신은 지우지 않는다. (3 남김)
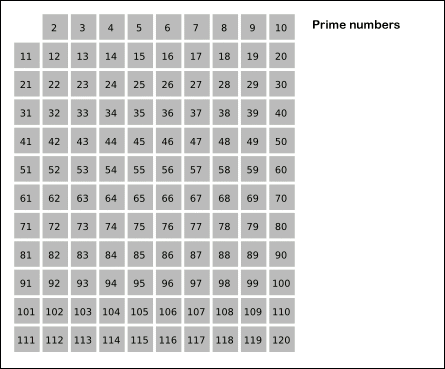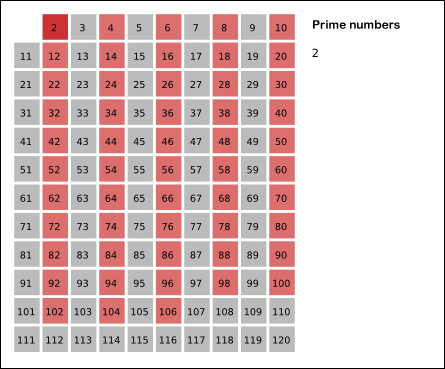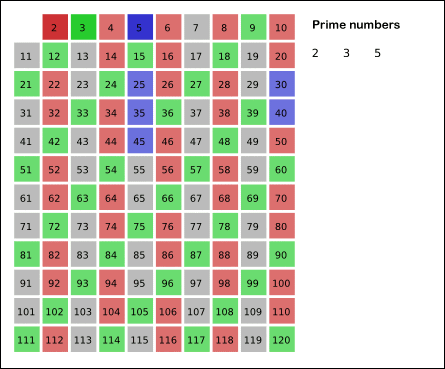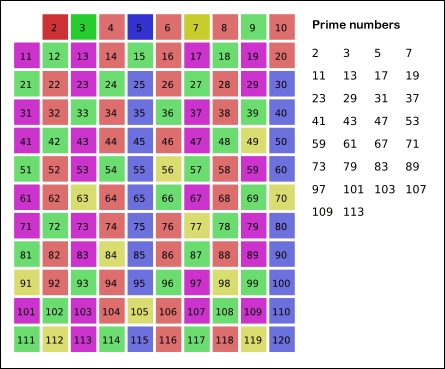
- 숫자를 1씩 늘려가며 N의 제곱근까지 반복한다. (120의 제곱근 = 10.95... => 10까지만 반복)
- N의 제곱근까지만 반복하는 이유
: N의 제곱근 이상의 숫자를 제곱한 값은 N보다 크기 때문에 더 이상의 연산은 의미가 없기 때문
ex) 120의 제곱근 = 10.95... [120의 제곱근보다 큰 숫자인 11의 제곱은 121이다. 121은 범위에서 벗어나기 때문에 의미 X]
- N의 제곱근까지만 반복하는 이유
- 반복문이 끝나고 배열에 남아있는 숫자는 모두 소수이다.
🎈 사용 예시 > 백준 1929번 : 소수 구하기
문제
M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
출력
한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다.
예제 입력
3 16
예제 출력
3
5
7
11
13
답
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int M = sc.nextInt();
int N = sc.nextInt();
int[] A = new int[N + 1];
// 2부터 N까지의 index를 가지는 배열의 각 index에 index값을 삽입
for (int num = 2; num <= N; num++) {
A[num] = num;
}
// 2부터 N의 제곱근까지 반복
for (int i = 2; i <= Math.sqrt(N); i++) {
// 요소값이 0이면 지워진 것으로 판별
if (A[i] == 0) {
continue;
}
// i의 배수를 배열에서 모두 지움
for (int j = i + i; j <= N; j = j + i) {
A[j] = 0;
}
}
// 최소 범위부터 시작하여, 요소가 0이 아니면 소수로 판별
for (int i = M; i <= N; i++) {
if (A[i] != 0) {
System.out.println(A[i]);
}
}
}
}
고대 그리스 수학자 에라토스테네스가 발견한 '에라토스테네스의 체'는 2부터 N까지의 범위에서 소수를 구하는 알고리즘이다.
소수를 판별하는 문제에서 매우 유용하게 사용할 수 있다.
1부터 120까지의 숫자중에서 소수인 숫자를 구하려면 어떻게 해야할까?
1부터 120까지 1씩 숫자를 늘려가며 소수인지 판별할 수도 있겠지만 '에라토스테네스의 체' 알고리즘을 사용하면 보다 빠르게 답을 구할 수 있다. 참고로 '에라토스테네스의 체'의 시간 복잡도는 O(n log(logn)) 이다.
'에라토스테네스의 체'의 핵심은 배열에서 소수의 배수를 모두 제거하고 남은 숫자는 모두 소수라는 성질을 이용한 것이다. 아래의 gif를 보자.

- 우선 2부터 N까지의 숫자를 저장하는 배열을 선언한다. 2부터 시작하는 이유는 1은 소수가 아니기 때문이다.
- 소수 : 1과 자신을 제외한 어떠한 자연수로도 나누어 떨어질 수 없는 수.
- 배열 범위 내에 있는 2의 배수를 모두 지운다. 자기 자신은 지우지 않는다. (2는 남김)
- 2 다음에 지워지지 않은 숫자의 배수를 모두 지운다. 마찬가지로 자기 자신은 지우지 않는다. (3 남김)
- 숫자를 1씩 늘려가며 N의 제곱근까지 반복한다. (120의 제곱근 = 10.95... => 10까지만 반복)
- N의 제곱근까지만 반복하는 이유
: N의 제곱근 이상의 숫자를 제곱한 값은 N보다 크기 때문에 더 이상의 연산은 의미가 없기 때문
ex) 120의 제곱근 = 10.95... [120의 제곱근보다 큰 숫자인 11의 제곱은 121이다. 121은 범위에서 벗어나기 때문에 의미 X]
- N의 제곱근까지만 반복하는 이유
- 반복문이 끝나고 배열에 남아있는 숫자는 모두 소수이다.
🎈 사용 예시 > 백준 1929번 : 소수 구하기
문제
M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.
출력
한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다.
예제 입력
3 16
예제 출력
3
5
7
11
13
답
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int M = sc.nextInt();
int N = sc.nextInt();
int[] A = new int[N + 1];
// 2부터 N까지의 index를 가지는 배열의 각 index에 index값을 삽입
for (int num = 2; num <= N; num++) {
A[num] = num;
}
// 2부터 N의 제곱근까지 반복
for (int i = 2; i <= Math.sqrt(N); i++) {
// 요소값이 0이면 지워진 것으로 판별
if (A[i] == 0) {
continue;
}
// i의 배수를 배열에서 모두 지움
for (int j = i + i; j <= N; j = j + i) {
A[j] = 0;
}
}
// 최소 범위부터 시작하여, 요소가 0이 아니면 소수로 판별
for (int i = M; i <= N; i++) {
if (A[i] != 0) {
System.out.println(A[i]);
}
}
}
}
