우리가 자주 사용하는 반복문, 정렬 알고리즘, 검색 알고리즘, 재귀 함수 등은 입력값에 따라 해당 알고리즘의 실행시간이 증가하게 된다. 이를 점근적 실행시간(asymptotic runtime)이라고 한다. 점근적 측정의 지표로 시간 복잡도 또는 공간 복잡도를 사용할 수 있다.
반대로 입력 값의 증가와 상관없이 항상 같은 실행 시간을 갖는 것을 상수 시간(constant runtime) - O(1) 이라고 한다.
시간 복잡도 표기법 종류
알고리즘의 효율성을 단순하게 구분하면 '최고의 경우', '최악의 경우', '평균적인 경우'의 세가지 측면에서 생각할 수 있다.
시간 복잡도 또한 이러한 세가지 측면에 따라 다르게 표기한다.
- Big-Ω(빅 오메가) 표기법 - 알고리즘이 최고의 성능을 낼 수 있도록 특별한 조건을 충족하는 최상의 경우
- Big-θ(빅 세타) 표기법 - 최상의 경우와 최악의 경우의 중간으로, 평균적인 실행시간을 표기한다.
- Big-O(빅 오) 표기법 - 알고리즘이 가장 오래걸릴 수 있는 실행 시간을 표기한다. 다시 말해 점근적 실행시간의 상한선을 말한다. 최소한의 성능을 알 수 있기 때문에 성능평가의 지표로 많이 사용한다.
시간 복잡도를 표기하는 방법으로 가장 많이 사용하는 것이 바로 '빅 오 (Big-O) 표기법'이다.
Big-O 시간 복잡도 종류
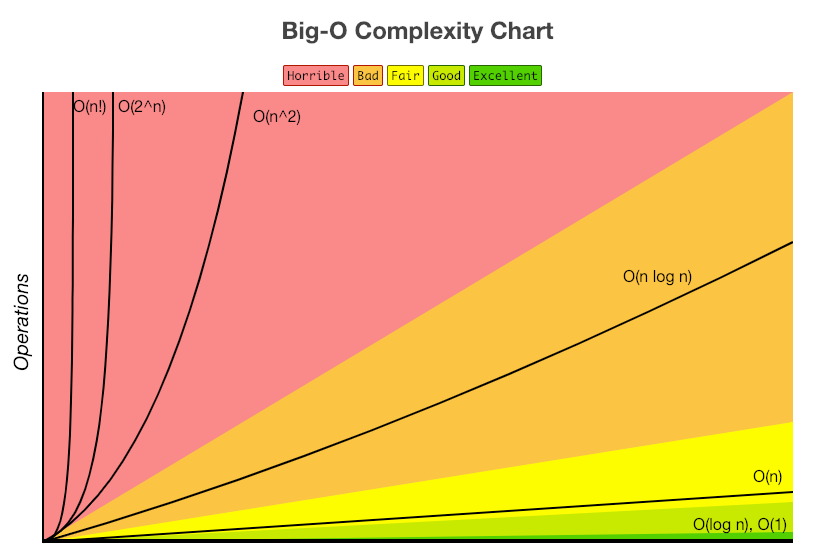
위 도표는 빅 오 시간에 따른 성능을 도표화 한 것이다. 빨간색에 가까워질수록 성능이 나쁘며 초록색에 가까워질수록 성능이 좋다. O(n!), O(n^2)은 성능이 끔직하다고 여겨지므로 다른 알고리즘을 고려해야 할 것이다. O(nlogn)은 O(n!)보다는 낫고, O(logn)과 O(1)은 좋은 성능을 보이는 것을 알 수 있다.

이처럼, 입력값이 증가될 수록 빅 오 시간에 따라 성능이 확연하게 차이나는 것을 알 수 있다.
📌빅 오 표기법에서 표현하는 시간 복잡도의 종류별 특징은 다음과 같다.
O(1)
빅 오 표기법에서 표현할 수 있는 최상의 성능을 나타내며 상수 시간이라고도 한다. 입력값의 개수와 상관없이 항상 같은 실행 시간을 가진다. (입력값의 개수가 성능에 영향을 끼치지 않는다.)
// 1. 상수 반환
return 23;
// 2. 인덱스를 활용한 배열 접근
int[] car = new int[10];
int thirdCar = cars[3];
// 3. 큐의 peek() 메서드 실행
Car car = cars.peek();다음은 O(1) 시간 복잡도의 예시이다. 위 예시 코드의 공통점은 코드라인 실행 시간이 다른 입력값에 전혀 영향을 받지 않는다는 점이다. 배열에 접근하는 시간은 배열의 요소 개수와 관계가 없고, Queue의 peek() 메서드의 실행 시간도 얼마나 많은 요소가 헤드와 연결되어 있는지는 전혀 중요하지 않다.
O(logn)
입력에 따라 실행 시간이 증가하는 시간 복잡도 표현에서 최상의 성능을 가진다. 이진 검색(Binary Search)와 같이 여러 단계에 걸쳐 입력을 절반으로 줄이는 알고리즘은 대부분 빅 오를 O(logn)으로 표현할 수 있다.
O(n)
주어진 입력값의 개수에 따라 실행 시간이 선형적으로 증가하기때문에 선형 시간이라고도 한다. 한마디로 최악의 경우에서 입력값이 N개이면 n만큼 실행 시간이 늘어나는 것을 말한다.
for (int i = 0; i< a.length; i++) {
// logic
}위의 예시 코드에서 a는 배열이다. for 문은 'a' 라는 배열의 크기에 따라 선형적으로 실행시간이 증가한다. 이와 같은 경우의 시간 복잡도를 O(n)으로 표기할 수 있다.
O(nlogn)
퀵 정렬, 병합 정렬과 같은 많은 정렬 알고리즘의 실행 시간은 O(nlogn)이다. 재귀적으로 동작하는 알고리즘이 많이 포함되며 분할 정복 카테고리로 분류되는 알고리즘의 실행 시간도 O(nlogn)이다.
O(n^2)
버블 정렬과 같은 비효율적인 알고리즘이 이에 해당한다. 같은 입력값을 2중으로 반복하는 for문도 O(n * n = n^2)로 나타낼 수 있다.
O(2^n)
fibonacci 수열을 같은 재귀함수로 계산하는 과정을 O(2^n)으로 나타낼 수 있다.
O(n!)
성능적으로 최악의 알고리즘이다. 입력 값이 조금만 커져도 실행 시간이 기하급수적으로 상승한다.
Big-O 표기법의 기본 규칙
Big-O 표기법은 다음과 같은 기본 규칙을 가지고 있다.
- 상수 제외 : O(2n) → O(n)
- 비우세항 제외 : O(n + n!) → O(n!)
- 여러개의 입력 데이터가 있을 때 변수를 각각 다르게 설정
- 서로 다른 단계를 종합하거나 곱함.
1. 상수 제외
int[] a = new int[n];
int countHello = 0;
int countWorld = 0;
for (int i=0; i< a.length; i++) {
countHello++;
countWorld++;
}int[] a = new int[n];
int countHello = 0;
int countWorld = 0;
for (int i=0; i< a.length; i++) {
countHello++;
}
for (int i=0; i< a.length; i++) {
countWorld++;
}다음의 두 예시 코드 중 첫 번째 코드는 for 문을 1개만 사용하지만 내부적으로 2줄의 코드가 반복된다. 두번째 코드는 for 문을 2개 사용하고 한줄씩의 코드만 반복된다.
따라서 첫 번째 코드는 O(n)이고 두 번째 코드는 O(n + n = 2n)이라고 생각하기 쉽다.
하지만 실제로 두 코드의 시간 복잡도는 O(n)으로 같다.
- 빅 오 표기법의 목표는 입력 크기에 관한 실행 시간 증가율을 표현하고 실행 시간이 어떻게 확장되는지 표현하는 것이다.
- 코드 구문의 개수를 세는것이 아님.
따라서 같은 반복문이 두 번 실행되더라도 입력 크기에 대한 실행 시간 증가율은 같다. 물론, 같은 반복문이 유의미한 횟수로 (ex - 100,000,000) 반복되면 당연히 실행시간에 영향이 가겠지만 이런 부분은 고려하지 않는다.
만약 for 문이 중첩된다면?
int[] a = new int[n];
for (int i=0; i< a.length; i++) {
for (int j=0; j< a.length; j++) {
// logic
}
}n 번의 반복문이 다시 n번 반복되는 형태이므로 n * n = O(n^2)로 나타낼 수 있다.
복잡하게 생각 할 것 없다. 단순히 표기법에서 상수를 제외하면 된다.
2. 비우세항 제외
int[] a = new int[n];
int countHello = 0;
int countWorld = 0;
//O(n)
for (int i=0; i< a.length; i++) {
countHello++;
countWorld++;
}
//O(n^2)
for (int i=0; i< a.length; i++) {
for (int j=0; j< a.length; j++) {
// logic
}
}다음과 같은 코드에서 첫 번째 for 문은 O(n)의 시간 복잡도를 가지며, 두 번째 for문은 O(n^2)의 시간 복잡도를 가진다.
예시 코드의 시간 복잡도를 n + n^2 라고 생각할 수 있다. 하지만, 실행 시간 증가율은 시간 복잡도가 더 큰 n^2에 의해 결정되기 때문에 n은 비우세항이라고 할 수 있다. 즉, 같은 입력 값에 대해 여러개의 시간 복잡도가 더해지는 형태에서 가장 시간 복잡도가 큰 항을 제외한 나머지는 제외한다.
따라서, 위 코드의 시간 복잡도는 O(n^2)이다.
- O(n! + 3n) -> 상수와 비우세항 제외 -> O(n!)
- O(nlogn + logn + 2n) -> 상수와 비우세항 제외 -> O(nlogn)
3. 여러개의 입력 데이터가 있을 때 변수를 각각 다르게 설정
int[] a = new int[n];
int[] b = new int[m];
// 입력 데이터가 다른 2개의 for 문
for (int i=0; i< a.length; i++) {
// logic
}
for (int i=0; i< b.length; i++) {
// logic
}예시 코드처럼 각기 다른 입력 값에 따라 실행 시간이 각각 증가하는 알고리즘이 있을 수 있다. 이 때, 해당 코드의 시간 복잡도를 단순히 O(n)으로 표기한다면 n은 a를 의미할지, b를 의미할지 나타낼 수 없다. 또한 각기 다른 입력값의 증가에 따른 실행 시간 증가율도 반영되지 못한다.
빅 오는 a의 실행 시간과 b의 실행 시간을 모두 반영해야한다. 따라서, 빅 오는 O(a + b)로 나타낼 수 있다.
여기서도 당연히 비우세항을 제거할 수 있다. O(a + b + a^2) -> O(a^2)
4. 서로 다른 단계의 합 또는 곱
int[] a = new int[n];
int[] b = new int[m];
// 입력 데이터가 다른 2개의 중첩 for 문
for (int i=0; i< a.length; i++) {
for (int j=0; j< b.length; j++) {
// logic
}
}예시 코드에서 두 for 문은 각자 다른 입력값에 따라 반복되는 횟수가 달라진다. 따라서, 이는 a * b 와 같으므로 빅 오는 O(a*b) 로 표기할 수 있다. 3번과 연결되는 내용으로, 실행 시간 증가율에 영향을 미치는 입력 데이터가 2개 이상 있을 경우 각 입력에 대해 별도의 변수를 사용하여 나타내야한다.
💡실행 시간의 빅 오 분석에서 알고리즘을 합하거나 곱하는 기준
- 서로 다른 알고리즘이 순차적 / 동기적으로 실행되지만 분리된 형태일 때 실행 시간을 더한다.
- 서로 다른 알고리즘이 묶여져있는 형태 (A 작업을 할 때마다 B 작업을 할 때)일 때 실행 시간을 곱한다.
참고
- https://codermun-log.tistory.com/235
- 자바 코딩인터뷰 완벽 가이드 (안겔 레오나르드 저 / 시진 옮김)
